光流子---移动目标检测 - keloy的博客

作者在 2009-12-24 09:53:48 发布以下内容

首先，我们定义什么是光流子（Optical flow）：维基上说：Optical flow or optic flow is the pattern of apparent motion of objects, surfaces, and edges in a visual scene caused by the relative motion between an observer and the scene.（光流子就是指在观察者和场景做相互运动时在运动的物体表面或者边上产生的一种运动亮度的模式。）我相信大家看了后和我一样都是晕的，但光流就是这个东西。

1.光流子的数学定义：

设I(x,y,t)是（x,y）像素点在t时刻的强度 $δ x$ , $δ y$ ， $δ t某一时刻非常短的时刻的位移，$

I (x, y, t) = I (x + δ x, y + δ y, t + δ t)

用泰勒方程展开上面的方程

H.O.T. 为泰勒展开式的高皆无穷小，所以上式的可以表示为：

然后对其作关于t的偏导：

改写上式可得

$V x, V y$ 就是点 $x$ ， $y$ 在t时刻的光流 $I (x, y, t)$ and , and 为期灰度梯度写为 $I x$ , $I y$ $I t$

所以：

I x V x + I y V y = - I t

由上式可以看出，我们这里有两个未知量 $V x, V y$ ，所以不能估计出其结果。

这时我们引入一个约束方程。就得到了光流子的Horn–Schunck method解法

这个约束方程的意思就是，要使得这个光流的平滑度和本身的偏差最小，这时光流就变成了求接上式的局部最小值。这时我们要用到“欧拉-拉格朗日方程”。

付：“欧拉-拉格朗日方程”

设 $f=f(x,\ y,\ z)$ ，以及 $f_y,\ f_z$ 在 $[a,\ b]\times\mathbb{R}^2$ 中连续，并设泛函

$J(y)=\int_a^b f(x, y(x), y'(x))dx$ 。

若 $y\in C^1[a,\ b]$ 使得泛函 $J (y)$ 取得局部极值，则对于所有的，

$\frac{d}{dx}\frac{\partial}{\partial y'}f(x, y, y')=\frac{\partial}{\partial y}f(x, y, y')$ 。

推广到多维的情况，记

，

。

若使得泛函取得局部极值，则在区间内对于所有的，皆有

。

为了使大家都能看懂我将方差方程改写为：

由欧拉-拉格朗日方程将方差方程，改写为

$\frac{\partial L}{\partial u} - \frac{\partial}{\partial x}\frac{\partial L}{\partial u_x} - \frac{\partial}{\partial y}\frac{\partial L}{\partial u_y} = 0$

$\frac{\partial L}{\partial v} - \frac{\partial}{\partial x}\frac{\partial L}{\partial v_x} - \frac{\partial}{\partial y}\frac{\partial L}{\partial v_y} = 0$

化简之后就变为：

I x (I x u + I y v + I t) - α 2 Δ u = 0

I y (I x u + I y v + I t) - α 2 Δ v = 0

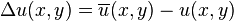其中 $\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$ ，由Laplace operator，估计可知， $\Delta u(x,y) = \overline{u}(x,y) - u(x,y)$ ，其中 $\overline{u}(x,y)$ 为（x,y）光流场的平均值。这时，公式就变为求解如下方程组。

$(I_x^2 + \alpha^2)u + I_xI_yv = \alpha^2\overline{u}-I_xI_t$

变性之后就变成了

$u^{k+1}=\overline{u}^k - \frac{I_x(I_x\overline{u}^k+I_y\overline{v}^k+I_t)}{\alpha^2+I_x^2+I_y^2}$

注意，这里，由于u（x，y）由其领域产生，就产生了迭代，于是上式就变成了迭代方程。Ix,Iy,It可以用相邻两张像素图片估计得到。

公式推导完了。

大概的方法就是这样，通过迭代方法产生的光流场。