作者在 2015-10-12 15:59:23 发布以下内容
|
Walls
Description
In a country, great walls have been built in such a way that every great wall connects exactly two towns. The great walls do not cross each other. Thus, the country is divided into such regions that to move from one region to another, it is necessary to go through a town or cross a great wall. For any two towns A and B, there is at most one great wall with one end in A and the other in B, and further, it is possible to go from A to B by always walking in a town or along a great wall. The input format implies additional restrictions.
There is a club whose members live in the towns. In each town, there is only one member or there are no members at all. The members want to meet in one of the regions (outside of any town). The members travel riding their bicycles. They do not want to enter any towns, because of the traffic, and they want to cross as few great walls as possible, as it is a lot of trouble. To go to the meeting region, each member needs to cross a number (possibly 0) of great walls. They want to find such an optimal region that the sum of these numbers (crossing-sum, for short) is minimized. 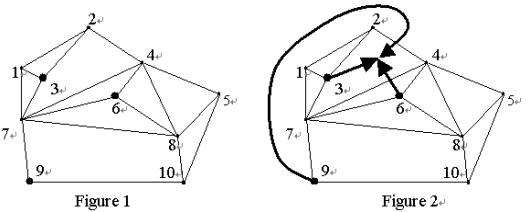 The towns are labeled with integers from 1 to N, where N is the number of towns. In Figure 1, the labeled nodes represent the towns and the lines connecting the nodes represent the great walls. Suppose that there are three members, who live in towns 3, 6, and 9. Then, an optimal meeting region and respective routes for members are shown in Figure 2. The crossing-sum is 2: the member from town 9 has to cross the great wall between towns 2 and 4, and the member from town 6 has to cross the great wall between towns 4 and 7. You are to write a program which, given the towns, the regions, and the club member home towns, computes the optimal region(s) and the minimal crossing-sum. Input
Your program is to read from standard input. The first line contains one integer: the number of regions M, 2 <= M <= 200. The second line contains one integer: the number of towns N, 3 <= N <= 250. The third line contains one integer: the number of club members L, 1 <= L <= 30, L <= N. The fourth line contains L distinct integers in increasing order: the labels of the towns where the members live.
After that the input contains 2M lines so that there is a pair of lines for each region: the first two of the 2M lines describe the first region, the following two the second and so on. Of the pair, the first line shows the number of towns I on the border of that region. The second line of the pair contains I integers: the labels of these I towns in some order in which they can be passed when making a trip clockwise along the border of the region, with the following exception. The last region is the "outside region" surrounding all towns and other regions, and for it the order of the labels corresponds to a trip in counterclockwise direction. The order of the regions gives an integer labeling to the regions: the first region has label 1, the second has label 2, and so on. Note that the input includes all regions formed by the towns and great walls, including the "outside region". Output
Your program is to write to standard output. The first line contains one integer: the minimal crossing-sum.
Sample Input 10 10 3 3 6 9 3 1 2 3 3 1 3 7 4 2 4 7 3 3 4 6 7 3 4 8 6 3 6 8 7 3 4 5 8 4 7 8 10 9 3 5 10 8 7 7 9 10 5 4 2 1 Sample Output 2 Source |
题意:在一个国家里
所有的城镇被城墙分割
因此国家被分为几个区域
从一个区域到另一个区域必须通过城镇或者穿过城墙
每两个城市之间最多只有一个城墙
这里有一个俱乐部,俱乐部的人住在城镇里
这个城镇最多只有一个人
成员们打算在某个区域里开会
他们不想进入城市
并且他们想爱你个尽量少的穿越城墙
为了开会,每个成员都要穿越一定数量的城墙
他们想要每个人穿越城墙数之和最小
城市被标记为1到n
计算出最有区域和最小交叉和
M个区域 2 200
n歌城市 3 250
l成员数 1 30
每个成员居住的城市
思路:把区域当成结点,当两个区域有公共边的时候,那么久说明这两个区域相邻,既有边。如此建图后跑一次floyd就可以知道任意两个结点的最短路了,然后枚举每个聚会区域,再枚举每个俱乐部点的相邻区域,求每个俱乐部点到聚会区域的最少翻墙数,求得sum,并和ans取min就是ans了
#include<stdio.h>
#include<string.h>
#include <iostream>
using namespace std;
#define maxn 330
int edge[maxn][maxn];
int markedge[maxn][maxn];
int mapi[maxn][maxn];
int secondv,n,m,clubsum,firstv,sum;
int club[maxn];
#define inf INT_MAX
void floyd()
{
for(int i=0; i<m; i++)
mapi[i][i]=0;
for(int k=0; k<m; k++)
{
for(int i=0; i<m; i++)
{
if(mapi[i][k]!=-1)
{
for(int j=0; j<m; j++)
{
if(mapi[k][j]!=-1)
{
if(mapi[i][j]==-1||mapi[i][j]>mapi[i][k]+mapi[j][k])
{
mapi[i][j]=mapi[i][k]+mapi[k][j];
}
}
}
}
}
}
}
int main()
{
while(~scanf("%d",&m))
{
int tmpv,tmpedge;
scanf("%d%d",&n,&clubsum);
for(int i=0; i<clubsum; i++)
scanf("%d",&club[i]);
memset(mapi,-1,sizeof(mapi));
memset(markedge,0,sizeof(markedge));
memset(edge,-1,sizeof(edge));
for(int i=0; i<m; i++)
{
scanf("%d%d",&sum,&firstv);
markedge[firstv][i]=1;
tmpv=firstv;
for(int j=1; j<sum; j++)
{
scanf("%d",&secondv);
markedge[secondv][i]=1;
tmpedge=edge[tmpv][secondv];
if(tmpedge!=-1)
{
mapi[tmpedge][i]=mapi[i][tmpedge]=1;
}
else
{
edge[tmpv][secondv]=edge[secondv][tmpv]=i;
}
tmpv=secondv;
}
tmpedge=edge[tmpv][firstv];
if(tmpedge!=-1)
{
mapi[tmpedge][i]=mapi[i][tmpedge]=1;
}
else
{
edge[tmpv][firstv]=edge[firstv][tmpv]=i;
}
}
floyd();
int ans=inf;
for(int i=0; i<m; i++)
{
int sum=0;
for(int j=0; j<clubsum; j++)
{
int mm=inf;
for(int k=0; k<m; k++)
{
if(markedge[club[j]][k])
{
mm=min(mm,mapi[k][i]);
}
}
sum+=mm;
}
ans=min(ans,sum);
}
printf("%d\n",ans);
}
}